高校受験が有利になる高校数学の公式

昨日から、国公立大学受験が始まりました。

大学受験は問題が一般公開されるのが遅いため、まだどこの問題も見ていませんが、まあ難しいですよね。

英語なんて語数が多すぎて眠くなってきます。

自分が受験するわけではないので、受験生と同じ熱量で問題と向き合うことはできませんが、皆さんは集中して頑張ってください！

『日本統一』を観ながら応援しています！

侠和会が暴力で日本を制覇する。

同じ展開だと分かっていますが、気がついたらもう60話まで観てしまいました。

『織田同志会』も面白かったし、Vシネたまらないです。

権力や知力、財力や魅力といったように、さまざまな力が存在しますが、結局は”暴力”こそが至高なんですね。

勉強に失敗して追い詰められることがあれば、まずは身体を鍛えて、学校や塾の先生を殴ってみてはいかがでしょうか。

少年院にお務めすることになりますが、これで君も”院卒”だ！

大卒より高学歴っすよ、カシラ！

誰のシマ

大学受験の数学では、（前提条件が間違っていない限り）大学数学で習う公式を使っても誰にも文句は言われません。

大学の基礎数学で習う公式を、高校数学の知識で証明させる問題もよくあります。

数Cに行列が含まれていた時代、空間ベクトルで外積を使って楽をしたり、そういった意味で大学受験は無法地帯です。

とはいえ、大学数学は公式を理解するのが大変なことにくわえ、その公式が成り立つ条件が複雑だったりすることもあって「高校数学において、大学数学の知識はあってもなくても大差ない」と言えます。

これと類似して、特に中学受験でよく聞く話ですが「どこまで中学数学を教えていいか」といったような、「どこまでの逸脱が許容範囲なのか」は悩みどころだと思います。

例えば「つるかめ算」といった「〜算」は、ほぼ全て”一次方程式と連立方程式”で片付きます。

理解が難しい単元ではないですし、中学数学に繋がるので、中学受験において方程式は必須の知識です。

上位中学を受験する生徒は、方程式の概念を理解していると思っていいです。

とはいえ、面積図や棒グラフなど、”手を動かして考える”ことは非常に重要なので、あくまで中受の算数を理解したうえで、応用として学ぶのが理想です。

中学数学において、中学受験に役立たない単元は1つもありません。

一見すると「平方根は必要なくない？」と考えてしまいますが、上位私立では、平方根を使わずに、その近似値を小数で求めさせる図形の応用問題が出題されます。

三平方の定理を知っていれば5秒、知らなければ超難問です。

つまり「中学受験において、中学数学の知識は点数に直結する」というのが事実であり、だからこそ、大手の中受専門塾はどこも予習を急ぐカリキュラムになっています。

対して、高校受験における高校数学の立ち位置ですが、大学受験と中学受験のちょうど中間のイメージです。

「知識があってもなくても変わらない」とは言えず、「点数に直結する」とも言えません。

三角関数を知っていても1点にもなりませんし、微積も無意味です。

そう考えると、どちらかと言えば大学受験と同じ立ち位置なのですが、「知っていると大きなアドバンテージが得られる公式」がいくつか存在します。

以下、そのうちのいくつかを紹介します。

組み合わせとコンビネーション

確率で頻出する最重要公式です。

これを知っているのと知らないのとでは、確率の難易度が激変します。

公立高校しか受験しないとしても、この公式だけは覚えておきましょう。

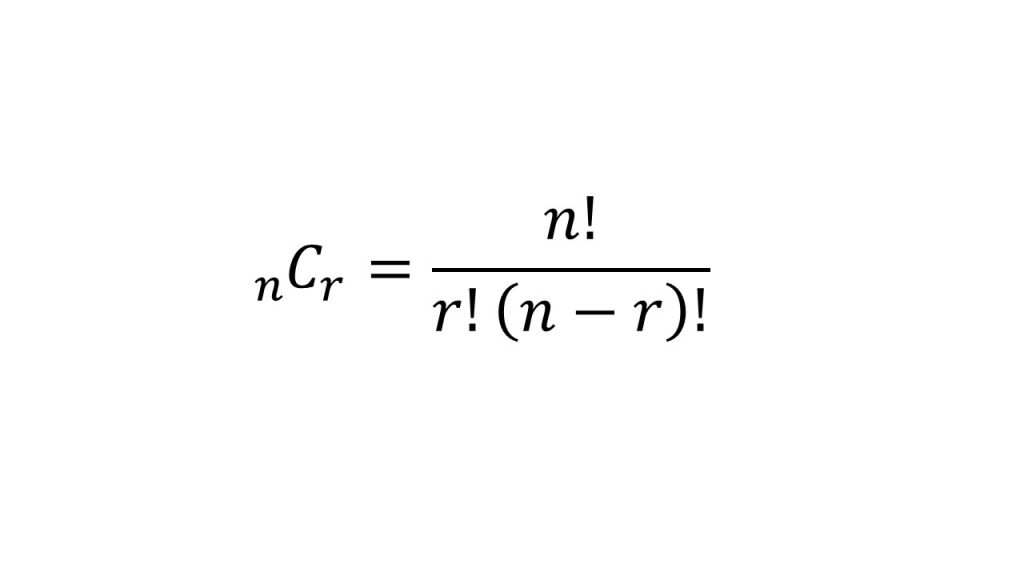
「n個の中からr個を選ぶ場合の数」を計算する式です。

難しいように見えますが、「分子はn〜(n-r+1)までの積」「分母はr〜1までの積」です。

例えば「6人の中から2人選ぶ場合の数」は「6×5/2×1=15通り」となります。

数学1Aで習う公式で、ネットにいくらでも解説があるので、詳しくは調べてください。

チェバ / メネラウスの定理

図形問題で頻出の重要公式です。

チェバ、メネラウスの利点は「補助線を引かなくても辺の比が求まる」だけですが、計算が楽になるので暗記を推奨します。

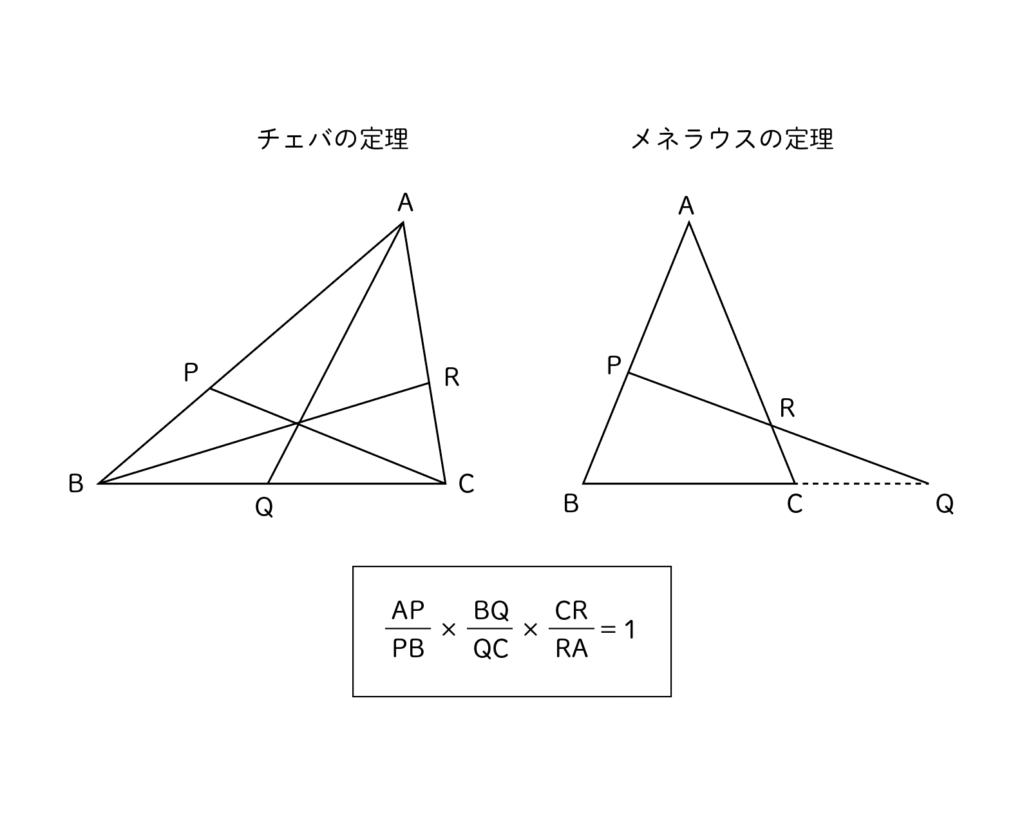
相似から導き出される公式なので、中学数学の範疇です。

解答欄に「チェバの定理より〜」と堂々と書いても大丈夫です。

ちなみに、チェバとメネラウスを使わない場合、平行線を引いて少しずつ辺の比を求めていきます。

円の方程式

早慶附属校をはじめ、上位私立でたまに見かける関数と円の重要公式です。

数学2Bで習う公式ですが、三平方の定理で簡単に証明できるため、これも中学数学の範疇です。

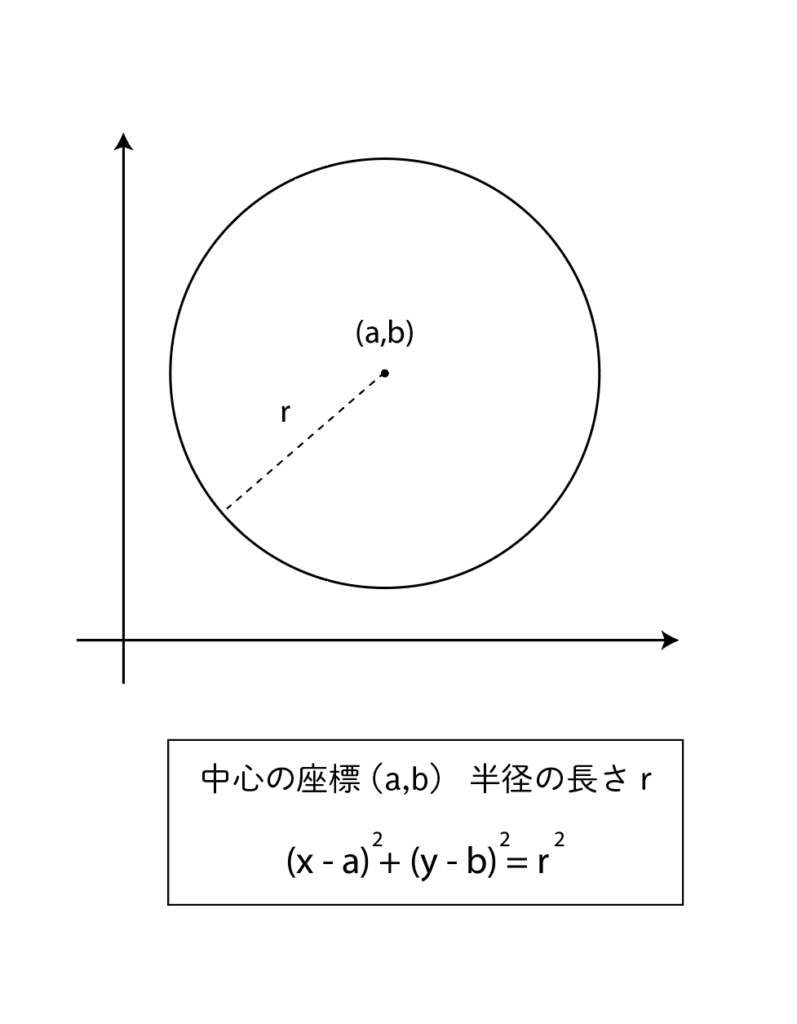
関数の難問といえば最終的には円が登場し、その半径や中心の座標、もしくは放物線との交点が問われます。

円の方程式を知っていれば、x,y座標にそれぞれ数値を代入するだけで機械的に答えが求まるので、予想以上に高校受験で役立ちます。

ちなみに、円の方程式を知らなければ「そんなの思いつかない」といった補助線や考え方が要求されるため、関数が苦手な生徒ほど効果を発揮する公式です。

以上の3つが「知っていると高校受験が有利になる高校数学の公式」です。

他にもいくつかありますが、とりあえず組み合わせの公式だけ覚えておけば何とかなります。

無料学習相談・体験授業の申し込みはこちら047-411-6247受付時間 17:00-21:30 [ 日除く ]

無料体験授業