【2026年】千葉県公立高校入試【数学解説】

千葉県公立高校入試、1日目が終わりました。

皆さん、手応えのほどはいかがでしたでしょうか。

早速ですが、いつものように数学の解説となります。

小問集合はテンプレから外れた問題で解きづらく、最後の文章題は日本語量が多く読解が大変だったのではないでしょうか。

難化しているとは言えませんが、解きづらい問題ではあったと思います。

以下、解説です。

大問1 小問集合

データの読み取り / 確率 / 作図 が例年のテンプレから少し外れており、取っつきにくかったかもしれません。

とは言え、確率はサイコロ2個の全事象36通りですし、全て書き出せば何とかなります。

大問2 関数

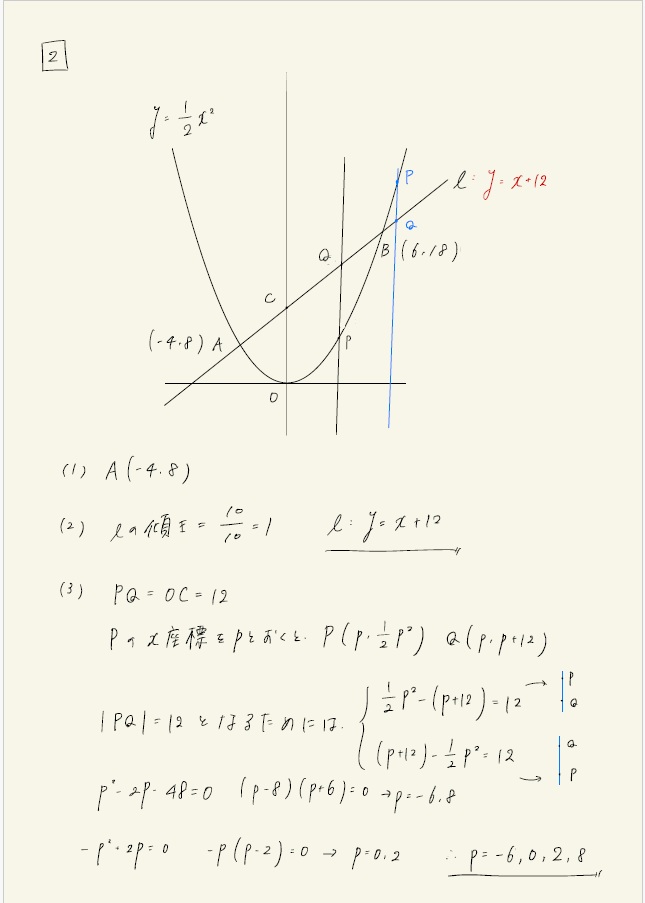
まあ簡単なんですけど、⑶は問題の図に線分QPが引かれていたことから、点Bの右側にあるパターンを思いつけなかった受験生が多いのではないでしょうか。

こういう小賢しいものを「子供だまし」と言いますが、中学生が相手であれば効果的かもしれません。

2次関数は最大次数が2次、2次方程式は最大で解の個数が2つ。

そう考えると、4つの解を要求されているのであれば、2次方程式を2つたてるという想像もしやすいです。

大問3 平面図形

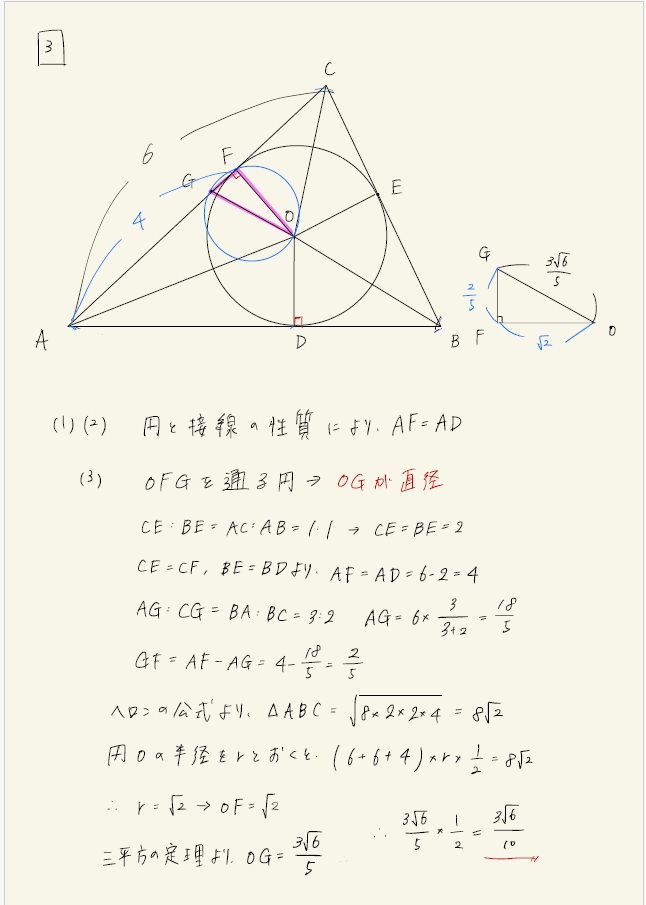
これもシンプルな問題ですね。

⑶については、OFGを通る円→OGが直径→OGの長さを求める問題に帰結する、ということが分かれば残りは作業です。

△ABCの面積は面倒なのでヘロンの公式で求めていますが、三平方でも何でも求められます。

証明問題については、そもそも出題意図が不明で、「円と接線の性質」でAF=ADが分かります。

これが許されないのであれば「円周角の定理」や「三平方の定理」を証明で使うことができなくなりますし、何のために出題したのでしょうか。

「円と接線の性質は中学範囲ではない」可能性もありますが、これを使わなければ⑶が非常に難しくなります。

仕方がないので知能レベルを出題者のレベルまで下げて考えると、無難なのは直角三角形の合同条件を使った証明ですかね。

低知能に合わせるのは疲れるので、もっと高知能な人間を出題者に選んでください。

せっかくですし、内心の性質を紹介しておきます。

非常に重要なのでこの機会に覚えておきましょう。

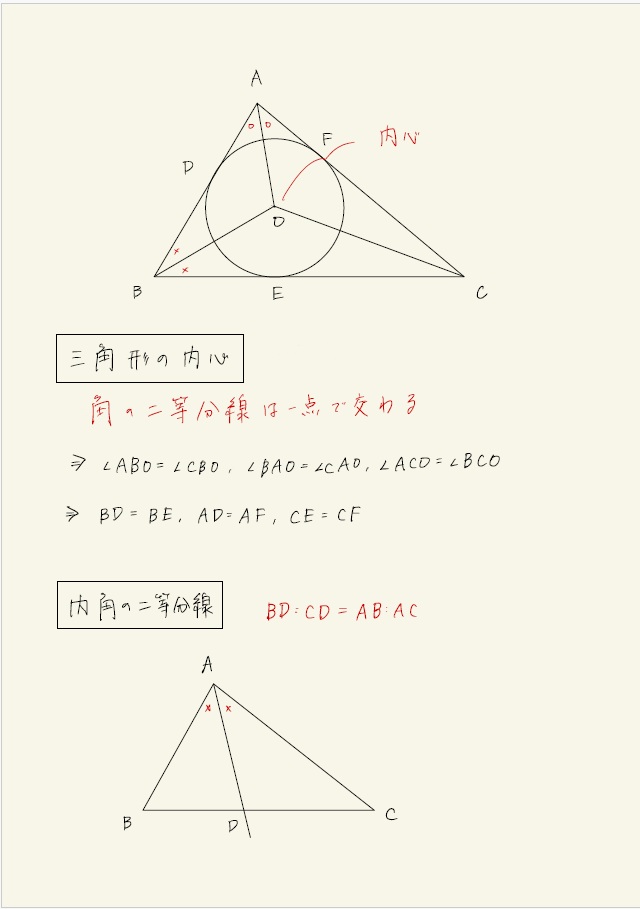
大問4 文章題

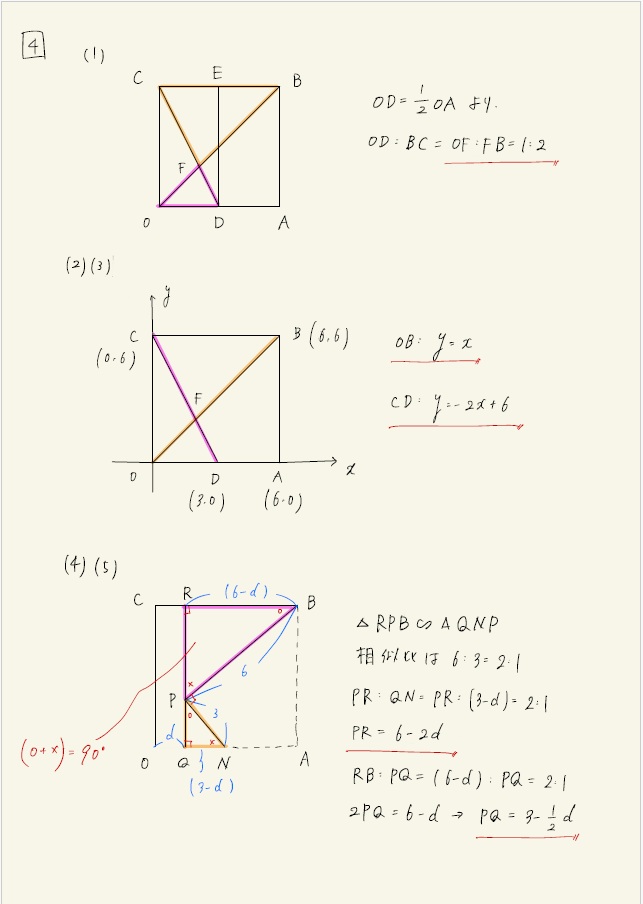
この問題も出題意図が不明です。

日本語が読めれば誰でも解けるので、あまりにも簡単すぎます。

後半なんてやっていることが全く同じですし。

5等分の折り方を説明させる記述問題なら面白い問題だったかもしれません。

恐らく、現代の中高生に不足している「読解力」を問う問題なのでしょうが、それは国語でやってください。

共通テストの数学は読解問題が出ても許されるんですよ。

国語を受験しない理系がいますからね。

だけど、これ公立高校受験なんです。

みんな国語も受験するんです。

「大学受験では数学でも読解が必要になるし、高校受験でも出題しておこう」という安直な思惑が透けて見えます。

まとめ

出題者のレベルの低さが顕著に出ている印象を受けました。

仮に第一志望の高校がこの問題を出してきたら、その時点で入学を拒否したくなるレベルです。

この問題を作った人間に教わっても、得られるものがあるとは思えないからです。

受験は「出題者は選ぶ側」「受験生は選ばれる側」という認識が強いですが、その逆も然りで、問題の質で学校の質が問われます。

中学、高校、大学のすべてに言えますが、良い学校は問題の質も高いです。

そういえば、公立高校の受験問題って誰が作っているのでしょうか。

興味がなかったので考えたこともありませんでしたが、これを機会に少し調べてみようと思います、まる

まだ理社が残っているので、今日は早く寝て、明日の受験に備えてください。

皆さんの成功を祈っています、エイメン！

無料学習相談・体験授業の申し込みはこちら047-411-6247受付時間 17:00-21:30 [ 日除く ]

無料体験授業